Цікавою і досить важливою для бізнесу була новація 2015 року — запровадження понижуючого коефіцієнта ЄСВ. Він уже знайшов відображення в новій формі звіту з ЄСВ і потихеньку почав застосовуватися платниками. У цій статті поговоримо про логіку коефіцієнта ЄСВ: чому виникають проблеми з округленням та як їх вирішити?
При обчисленні ЄСВ і перевірці, чи виконуються всі умови для застосування коефіцієнта, чимало платників зіткнулися з проблемою, що не виконується одна умова: середній внесок на одну особу виходить на кілька копійок меншим, аніж середній внесок за 2014 рік. Спробуймо з'ясувати, чому так відбувається, шляхом аналізу цього нового алгоритму.
Як ми визначаємо понижуючий коефіцієнт? Як співвідношення середньої зарплати на одного працівника в 2014 р. та середньої зарплати в поточному місяці 2015 р.
У статті, для наочності, братимемо конкретні цифри, уникаючи умовних позначень. Зроблені обчислення покажуть, що підприємству досить просто підставити в розрахунок свої власні цифри.
Припустімо, в 2014 р. середньомісячна база нарахування єдиного внеску на одну застраховану особу (якщо немає інших виплат, що оподатковуються ЄСВ, то це — середня заробітна плата) була 1314,80 грн, а на сьогодні база нарахування ЄСВ на одну застраховану особу за місяць становить 2000 грн. Очевидно, що зарплата збільшилася, і більше ніж на 20%. Якщо при цьому працівників на підприємстві не побільшало більш ніж на 200%, то підприємство має підстави починати обчислювати коефіцієнт, який застосовуватиметься до ставок ЄСВ. Коефіцієнт обчислюється так:
К= 1314,80 : 2000 = 0,6574.
Закон про ЄСВ вимагає скорочувати коефіцієнт до трьох знаків після коми. Тобто маємо 0,657.
Якщо ставка ЄСВ умовно становила 38%, то в 2014 р. ми сплачували в середньому на одного працівника: 1314,80 х 0,38 = 499,62 грн. При застосуванні коефіцієнта в 2015 р. отримуємо: 0,657 х 2000 х 0,38 = 499,32 грн. Ця сума є меншою від 499,62 грн, а отже, коефіцієнт застосовувати не можна. У чому проблема? Спробуймо проаналізувати її з математичного погляду. Об'єднаємо дві попередні формули, підставивши замість значення коефіцієнта 0,657 у другу формулу те, як ми його розраховували:
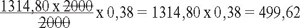
Як видно з наведеного, застосовуючи коефіцієнт, ми одночасно ділимо і множимо на поточну базу ЄСВ (базу в поточному місяці 2015 р.), у цьому випадку — 2000 грн. А тому це число за правилами елементарної математики можна скоротити.
Наведений аналіз проблеми дає нам такі три висновки:
1) середня сума ЄСВ за 2015 рік на одну особу після застосування коефіцієнта не залежить від середньої зарплати в поточному місяці;
2) ця сума не може бути меншою від середньої суми ЄСВ на одну особу в 2014 р. Вона може лише дорівнювати цій сумі;
3) проблема невідповідності цих сум виникає лише внаслідок передбаченого законом округлення при застосуванні коефіцієнта.
Ситуація є досить цікавою, адже скидається на те, що автори тексту закону спробували в ньому змінити математичні закони, які, як і закони природи, змінити неможливо. Проте нам доводиться рахуватися з наявністю в законі правила: спочатку мусимо обчислити коефіцієнт, округливши його до трьох знаків після коми, а відтак уже застосовувати його на практиці. І якщо отримана сума в розрахунку на одного працівника буде меншою від аналогічної суми за 2014 рік, то при застосуванні коефіцієнта вийде значна сума недоплати ЄСВ. А отже, маємо з'ясувати, як уникнути проблеми з округленням.
Як не дивно, в самій цій проблемі є своя логіка, і ця логіка — також математична.
Так, отриманий унаслідок розрахунку коефіцієнт майже завжди є довгим десятковим дробом і має більше трьох знаків після коми. Округлюючи дріб до трьох знаків, ми діємо відповідно до правила округлення: все, що в наступному розряді більше від 5, — округлюємо шляхом збільшення, все, що в наступному розряді нижче або дорівнює 5, — округлюємо шляхом зменшення.
Наприклад, 0,6573 та 0,6574 — округлюється до 0,657 (шляхом зменшення), а 0,6575 та 0,6576 — вже до 0,658 (шляхом збільшення).
Так от, у проблемі з округленням коефіцієнта спостерігається така логіка:
якщо при округленні ми зменшуємо коефіцієнт (відкидаємо десяткові знаки), то наприкінці виявиться, що сума ЄСВ у розрахунку на одного працівника є дещо меншою, ніж була в 2014 р. Справді, зменшуючи коефіцієнт, ми нібито зменшуємо суму ЄСВ. У цьому разі коефіцієнт застосовувати не можна буде.
І навпаки, коли при округленні ми збільшуємо коефіцієнт (округлення шляхом збільшення), отримана сума ЄСВ у розрахунку на одного працівника буде дещо більшою, ніж у 2014 р. У цьому разі, за дотримання решти умов, коефіцієнт можна застосовувати.
Запитання: чи можна округлення робити довільно? З одного боку, збільшуючи коефіцієнт, ми збільшуємо суму ЄСВ, а отже, нічого поганого не робимо. А з іншого — якби ми полічили правильно, то взагалі б не мали права на застосування коефіцієнта. Оскільки суми ЄСВ зазвичай є досить значними, строків давності немає, при фіскальному підході підприємство може отримати серйозні проблеми лише через неправильне округлення. Тому застосовувати цей шлях не рекомендуємо.
Виходом зі ситуації є підбір середньої зарплати з метою отримання коефіцієнта, який округлюється шляхом збільшення. Цей шлях є зовсім не проблемою для підприємств, які практикують гнучку зарплату (із прогресивкою, премією або іншою гнучкою складовою). А в разі коли виплачуються лише оклади, як правило, можна вийти зі ситуації шляхом збільшення окладу або перегляду системи оплати праці. Нагадаємо, що йдеться про середні величини (середню зарплату, середню суму ЄСВ з розрахунку на одного працівника).
Тому, підвищивши або зменшивши зарплату одному працівникові, ми можемо вплинути на розмір середньої зарплати, а отже, і на розмір коефіцієнта. При цьому збільшити зарплату доведеться не на велику суму, інколи достатньо буде кількох гривень, а економічний ефект через застосування понижуючого коефіцієнта очевидний.
Повернімося до вищерозглянутого прикладу. Нас не влаштовує обчислений коефіцієнт: К = 1314,80 : 2000,00 = 0,6574 = 0,657, бо він не може бути застосований через округлення шляхом зменшення.
Але, підвищивши середню зарплату на 1,23 грн, ми можемо досягнути ситуації, коли коефіцієнт округлюватиметься в бік збільшення, і проблема вирішиться.
К = 1314,80 : 2001,23 = 0,656995… = 0,657.
Обчислимо суму ЄСВ з розрахунку на одного працівника:
0,657 х 2001,23 х 0,38 = 499,63 грн.
Як бачимо, ця сума є більшою від суми ЄСВ на одного працівника за 2014 р., а отже, той самий коефіцієнт застосовувати можна.
Наголосимо, що побоюватися незначного підвищення зарплати не варто, адже, як ми з'ясували, сума ЄСВ усе одно залишається на рівні попереднього року (саме це і є сутністю коефіцієнта). А на розмірах утримань ПДФО і ЄСВ, а також ВЗ відповідні незначні збільшення відбиваються неістотно.
Завершуючи наш «математично-соцстрахівський екскурс», додатково зазначимо, що проблема виникла через розділення в законі моменту обчислення коефіцієнта та його застосування й обмеження округлень.
Тому законодавцеві слід рекомендувати спростити цей механізм розрахунку, адже перевірка на округлення в механізмі оподаткування справді виглядає несерйозно. Потрібного можна досягти об'єднанням формул, як ми зробили вище (в третій формулі), або видаленням цієї перевірки із закону взагалі. Адже правила застосування коефіцієнта є такими, що (якщо знехтувати округленням) сума ЄСВ у розрахунку на одного працівника дорівнює цій сумі за 2014 рік, що, по суті, і стимулює бізнес до підвищення зарплати.
Олексій КРАВЧУК, к. ю. н., доцент, аудитор
